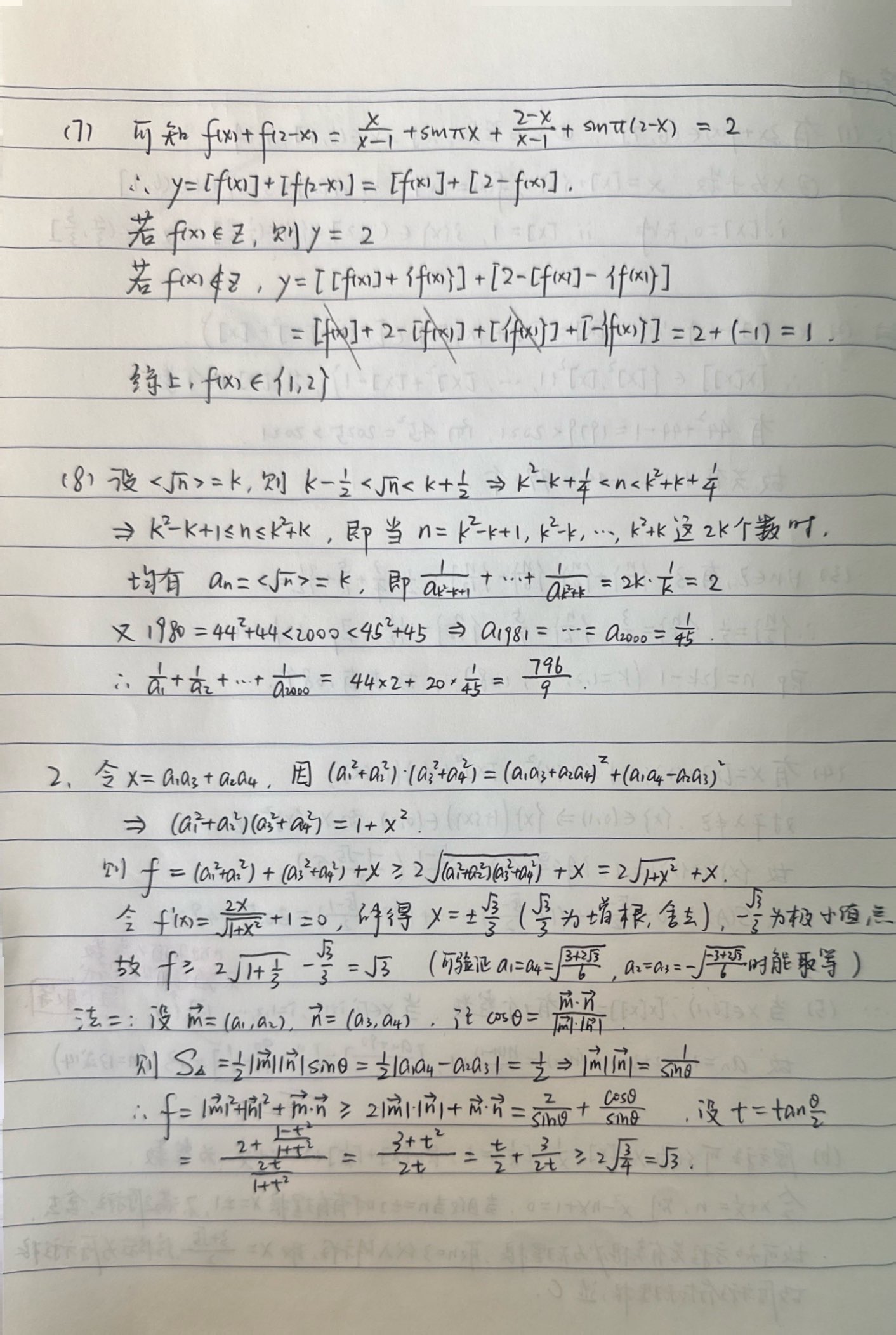几道题目
上次周练13的12题好像考了关于取整的题目,但题不在手边。这里整理了一些手边的有关取整的题目。
取整的题目其实不难,唯一需要的技巧就是利用$x=[x]+\{x\}$。有时候找规律、分类讨论也能出结果。
1.(1)定义$f(x)$表示不小于$x(x>0)$的最小整数.若$f(3x+f(x))=f(6.5)$,则正实数$x$的取值范围为__________.
(2)在$1,2,\cdots,2021$中,可以表示为$[x[x]] (x>0)$形式的数共有__________个.
(3)设正整数$n\leq2022$,且$\{\frac{n}{2}\}+\{\frac{n}{4}\}+\{\frac{n}{6}\}+\{\frac{n}{12}\}=3$.则这样的$n$共有__________个.
(4)正实数数列$A=\{a_1,a_2,\cdots,a_{100}\}$满足:对$\forall{x}\in{A},x\notin{Z}$但$x+\{x\}^2\in{Z}$(其中$\{x\}=x-[x]$),则$S(A)=a_1+a_2+\cdots+a_{100}$的最小值为__________.
(5)定义函数$f(x)=[x[x]]$,当$x\in[0,n),n\in\mathbf{N^{*}}$时,设函数$f(x)$的值域为$A$,记集合$A$中的元素个数为$a_n$,则$[\dfrac{a_n+90}{n}]$的最小值为__________.
(6)设$[x]$表示不超过$x$的最大整数,且$\{x\}=x-[x]$,则方程$\{x\}+\{\frac{1}{x}\}=1$( )
A. 方程无实根 B. 方程存在整数解
C. 方程存在无理数根 D. 方程有两个以上有理数根
(7)已知$f(x)=\dfrac{x}{x-1}+\sin{\pi{x}}$,则$y=[f(x)]+[f(2-x)]$的值域为__________.
(8)设$a_n=<\sqrt{n}>$,其中$< x >$表示与$x$最接近的整数,则$\dfrac{1}{a_1}+\dfrac{1}{a_2}+\cdots+\dfrac{1}{a_{2000}}$的值为__________.
2.设$a_1,a_2,a_3,a_4\in\mathbf{R}$且$a_1a_4-a_2a_3=1$,则$f={a_1}^2+{a_2}^2+{a_3}^2+{a_4}^2+a_1a_3+a_2a_4$的最小值为__________.
(提示:有$(a^2_1+a^2_2)(a^2_3+a^2_4)=(a_1a_3+a_2a_4)^2+(a_1a_4-a_2a_3)^2$)